「Shader」从零开始的VolumeRaymarching PART Ⅰ

Shader

噪声总体分为两类： 晶格噪声（Lattice based）

• 多数的噪声都为这种，梯度噪声（包括Perlin噪声， Simplex噪声，Wavelet噪声）和value噪声

点的噪声（Point based）

• 包括worley噪声；

Perlin噪声、Simplex噪声和Value噪声在性能上大致满足：Perlin噪声 > Value噪声 > Simplex噪声，Simplex噪声性能最好。Perlin噪声和Value噪声的复杂度是O(2n)O(2n)，其中n是维数，但Perlin噪声比Value噪声需要进行更多的乘法（点乘）操作。而Simplex噪声的复杂度为O(n2)O(n2)，在高纬度上优化明显。

Perlin noise

Perlin噪声原理是简单来说就是将坐标系划分成一块一块的晶格，之后在晶格的顶点处生成一个随机的梯度，通过与晶格顶点到晶格内点的向量进行点乘加权计算后得到噪声。

· 定义一个晶格结构，每个晶格的顶点有一个“伪随机”的梯度向量（其实就是个向量啦）。对于二维的Perlin噪声来说，晶格结构就是一个平面网格，三维的就是一个立方体网格。
· 输入一个点（二维的话就是二维坐标，三维就是三维坐标，n维的就是n个坐标），我们找到和它相邻的那些晶格顶点（二维下有4个，三维下有8个，n维下有2n2n个），计算该点到各个晶格顶点的距离向量，再分别与顶点上的梯度向量做点乘，得到2n2n个点乘结果。
· 使用缓和曲线（ease curves）来计算它们的权重和。在原始的Perlin噪声实现中，缓和曲线是s(t)=3t2−2t3s(t)=3t2−2t3，在2002年的论文6中，Perlin改进为s(t)=6t5−15t4+10t3s(t)=6t5−15t4+10t3。这里简单解释一下，为什么不直接使用s(t)=ts(t)=t，即线性插值。直接使用的线性插值的话，它的一阶导在晶格顶点处（即t = 0或t = 1）不为0，会造成明显的不连续性。s(t)=3t2−2t3s(t)=3t2−2t3在一阶导满足连续性，s(t)=6t5−15t4+10t3s(t)=6t5−15t4+10t3在二阶导上仍然满足连续性。

vec2 hash22(vec2 p)//the gradient vector
{
    p = vec2( dot(p,vec2(127.1,311.7)),
              dot(p,vec2(269.5,183.3)));
    return -1.0 + 2.0 * fract(sin(p)*43758.5453123);
}
float perlin_noise(vec2 p)
{
    vec2 pi = floor(p);
    vec2 pf = p - pi;
    vec2 w = pf * pf * (3.0 - 2.0 * pf);
    return mix(mix(dot(hash22(pi + vec2(0.0, 0.0)), pf - vec2(0.0, 0.0)), 
                   dot(hash22(pi + vec2(1.0, 0.0)), pf - vec2(1.0, 0.0)), w.x), 
               mix(dot(hash22(pi + vec2(0.0, 1.0)), pf - vec2(0.0, 1.0)), 
                   dot(hash22(pi + vec2(1.0, 1.0)), pf - vec2(1.0, 1.0)), w.x),
               w.y);
}

这里用到了一个hash函数来计算梯度，其实是一个叫哈希函数，可以避免掉使用fract(sin(p))导致的不同设备带来的巨大差别，具体函数的呈现可以跳转到乐乐老师的Hash without Sine (shadertoy.com)关于hash函数的记录

在解决了基础的Perlin noise之后，我们就可以通过不同的加和方式实现不同的效果，这里就用到了一个fbm（Fractal Brownian Motion） 分型布朗运动。其实是把不同的噪声在不同的频率下进行叠加，每一个噪声是一个octave。最经典的fbm做法

noise(p)+1/2noise(2p)+1/4noise(4p)+…

实现的效果类似山脉，石头的物体

如果把noise加一个绝对值

|noise(p)|+1/2|noise(2p)|+1/4|noise(4p)|+…

实现类似湍流的效果（火焰、云朵）turbulence公式

如果再把这个分型函数嵌套（每一次运算都在uv上加一个随机的seed）

 fbm(p+fbm(p+fbm(p))) 

在这个基础上，混合一点颜色，调整一下uv，就可以得到下面的这样的东西

value噪声

其实就是把Perlin噪声的梯度变成了伪随机值，不需要点乘，节省了很多计算量

  - 定义一个晶格结构，每个晶格的顶点有一个“伪随机”的值（Value）。对于二维的Value噪声来说，晶格结构就是一个平面网格，三维的就是一个立方体网格。

• 输入一个点（二维的话就是二维坐标，三维就是三维坐标，n维的就是n个坐标），我们找到和它相邻的那些晶格顶点（二维下有4个，三维下有8个，n维下有2n2n个），得到这些顶点的伪随机值。
• 使用缓和曲线（ease curves）来计算它们的权重和。同样，缓和曲线可以是s(t)=3t2−2t3s(t)=3t2−2t3，也可以是s(t)=6t5−15t4+10t3s(t)=6t5−15t4+10t3（如果二阶导不连续对效果影响较大时）。

  float value_noise(vec2 p)
    {
        vec2 pi = floor(p);
        vec2 pf = p - pi;

        vec2 w = pf * pf * (3.0 - 2.0 * pf);

        return mix(mix(hash21(pi + vec2(0.0, 0.0)), hash21(pi + vec2(1.0, 0.0)), w.x),
                   mix(hash21(pi + vec2(0.0, 1.0)), hash21(pi + vec2(1.0, 1.0)), w.x),
                   w.y);
    }

simplex噪声

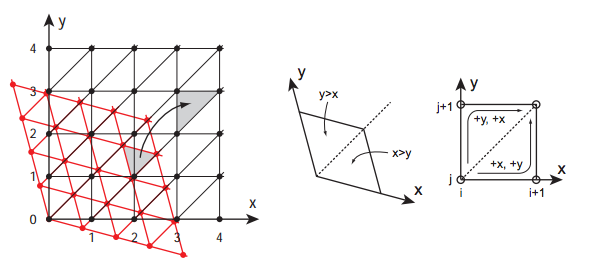
理解上是最复杂的噪声，理论上就是把perlin的晶格转化为了单体（三角），而这样的好处是对每一个点的特征点数更少，为n+1个，而在计算当中，我们是通过对于正方形的网格进行变形形成新网格实现的，而在贡献度计算当中，则采用了另外一种计算方法 (r^2−|dist|^2)4×dot(dist,grad)。其中r为0.5 x′=x+(x+y+...)⋅K1 y′=y+(x+y+...)⋅K1 其中，K1=(√(n+1)−1)/n n为维数。而这个逆转换就为K2=-(1/√(n+1)−1)/n

float simplex_noise(vec2 p)
{
    const float K1 = 0.366025404; // (sqrt(3)-1)/2;
    const float K2 = 0.211324865; // (3-sqrt(3))/6;

    vec2 i = floor(p + (p.x + p.y) * K1); //找到方格索引顶点（公式）

    vec2 a = p - (i - (i.x + i.y) * K2); //变形前输入点到原点的距离向量（公式）
    vec2 o = (a.x < a.y) ? vec2(0.0, 1.0) : vec2(1.0, 0.0); //判断在上还是下
    vec2 b = a - o + K2; //第二个单形顶点
    vec2 c = a - 1.0 + 2.0 * K2; // 第三个单形顶点

    vec3 h = max(0.5 - vec3(dot(a, a), dot(b, b), dot(c, c)), 0.0);//求出权重
    vec3 n = h * h * h * h * vec3(dot(a, hash22(i)), dot(b, hash22(i + o)), dot(c, hash22(i + 1.0))); //点乘求和

    return dot(vec3(70.0, 70.0, 70.0), n); //最终乘一个贡献度补偿回-1到1
}

Worley 噪声

相当于通过画网格，网格内随机取点得到距离场

  vec2 i_st = floor(st);
    vec2 f_st = fract(st);// Tile the space
    float m_dist = 1.;  // minimum distance
    vec2 m_point;
    for (int y= -1; y <= 1; y++) {
        for (int x= -1; x <= 1; x++) {
            // Neighbor place in the grid
            vec2 neighbor = vec2(float(x),float(y));
            vec2 point = random2(i_st + neighbor);
            point = 0.5 + 0.5*sin(iTime + 6.2831*point);
            vec2 diff = neighbor + point - f_st;
            float dist = length(diff);
            if( dist < m_dist ){
                m_dist = dist;
                m_point = point;
            }
        }
    }
    color += dot(m_point,vec2(.3,.6));//get different color of hole piece
    color += m_dist * 0.3;// Draw the min distance (distance field)
    color += 1.-step(.02, m_dist);// Draw cell center

一般的voroni距离场计算方法 而后来Inigo在2014年提出了让voronoi和常规噪声的融合方法，代码如下，

float voronoise( in vec2 p, float u, float v )
{
    float k = 1.0+63.0*pow(1.0-v,6.0);

    vec2 i = floor(p);
    vec2 f = fract(p);

    vec2 a = vec2(0.0,0.0);
    for( int y=-2; y<=2; y++ )
    for( int x=-2; x<=2; x++ )
    {
        vec2  g = vec2( x, y );
        vec3  o = hash3( i + g )*vec3(u,u,1.0);
        vec2  d = g - f + o.xy;
        float w = pow( 1.0-smoothstep(0.0,1.414,length(d)), k );
        a += vec2(o.z*w,w);
    }

    return a.x/a.y;
}

常用的噪声就差不多记录完了，基本都是在上面的基础上做变体。这里再贴一个3D的perlin noise的实现方法。

float noise( in vec3 x )
{
    vec3 i = floor(x);
    vec3 f = fract(x);
    f = f*f*(3.0-2.0*f);

    return mix(mix(mix( hash(i+vec3(0,0,0)), 
                        hash(i+vec3(1,0,0)),f.x),
                   mix( hash(i+vec3(0,1,0)), 
                        hash(i+vec3(1,1,0)),f.x),f.y),
               mix(mix( hash(i+vec3(0,0,1)), 
                        hash(i+vec3(1,0,1)),f.x),
                   mix( hash(i+vec3(0,1,1)), 
                        hash(i+vec3(1,1,1)),f.x),f.y),f.z);
}

本文参考：乐乐女神的噪声分析https://blog.csdn.net/candycat1992/article/details/50346469 iq大佬的博客https://iquilezles.org/www/articles/voronoise/voronoise.htm

作者： Ayse