「Houdini」关于旋转的粗浅理解 以及H中的定位方式

Houdini

在制作塔楼的瓦片的时候，遭遇到了法线的问题，copytopoint开始要应用三维旋转了，于是乎开始查文档和案例。总结了一下关于VEX中对旋转的表达同时也查了关于旋转的一些总体的表示方法。

旋转

常见的旋转的表示方法：矩阵（旋转矩阵），欧拉角，四元数。

1、矩阵 每一列表示旋转后的单位矢量方向

2、欧拉角： 将旋转分为roll（筒滚z），pitch（俯仰x），yaw（偏航y）三个轴向的三个维度，但是会产生万向锁问题——两轴重合损失自由度：有一个平行于x轴的向量，我们先将它饶y旋转直到它平行于z轴，这时，我们会发现任何饶z的旋转都改变不了向量的方向（废掉了一个方向的自由度），即万向节死锁。

3、四元数： 为了深入理解旋转，在这里简单的解释一下这个晦涩难懂的用法在几何空间的理解，理解的主要参考是知乎各个答主不同角度的解释，以及最重要的是有一个大神讲了相关的视频[四元数的可视化]（我反正也是一知半解，没有特别懂） （网上还有很多大佬有数学方面的解释，代数推导看了一遍，只能说勉勉强强能看明白，以后要当技术美术的人了就还是得回到图形化认知来，我这就简单说一下我粗浅的形象化认知。）

先普及四元数基本特点和一些基本的数学结论

（1）优点 四元数可以很方便插值，因为高维的球体连线代表的值之后在三维空间中就是均匀的旋转，而且表示的数字很少，只需3个数字来存储，计算速度也比矩阵快。

（2）特性与结论

q=[cosθ/2,sinθ/2 vector] 最终旋转结果是* a` = q a q **

其中，q*是q的共轭四元数——虚部取负。一般称之为“quaternion sandwich”。四元数的点乘是一般的计算方法，推导后可以优化成 q1q2=(st−u⋅v,sv+tu+u×v) st分别为q1q2的实部，uv分别为q1q2的虚部

p四元数就是四维空间的向量，虚部符合以下的规律

ij=−ji=k
jk=−kj=I
ki=−ik=j
i2=j2=k2=ijk=−1

观察一下这几组数，这几个条件——反交换律，三个数乘起来是1，不就是叉乘的结果么。也就是让 i,j,k 分别对应到三维坐标系的三个坐标轴方向的单位向量。这就是图形理解的基础。

（3）回归二维复数 首先要看到二维复数中，对于一维的点，乘以一个i就相当于在二维平面旋转90度，进一步推导出p= cosθ+isinθ，乘这个p，就是将（1，0）绕原点转θ度。p=[cosθ,sinθ]（当然，这个转完的东西1维的人只能看到变形的投影）

（4）回到四元数 四元数就是四维的实部和ijk三维虚部组成，四维超球（一个四维单位球）投影到三维空间就是占满了所有空间的一个体，实部大于0的就是三维单位球以内的空间，实部小于零就是外边，单位球就是实部等于0只有ijk的情况，我们就先叫它临界球（三维空间和四维空间的交界处）。

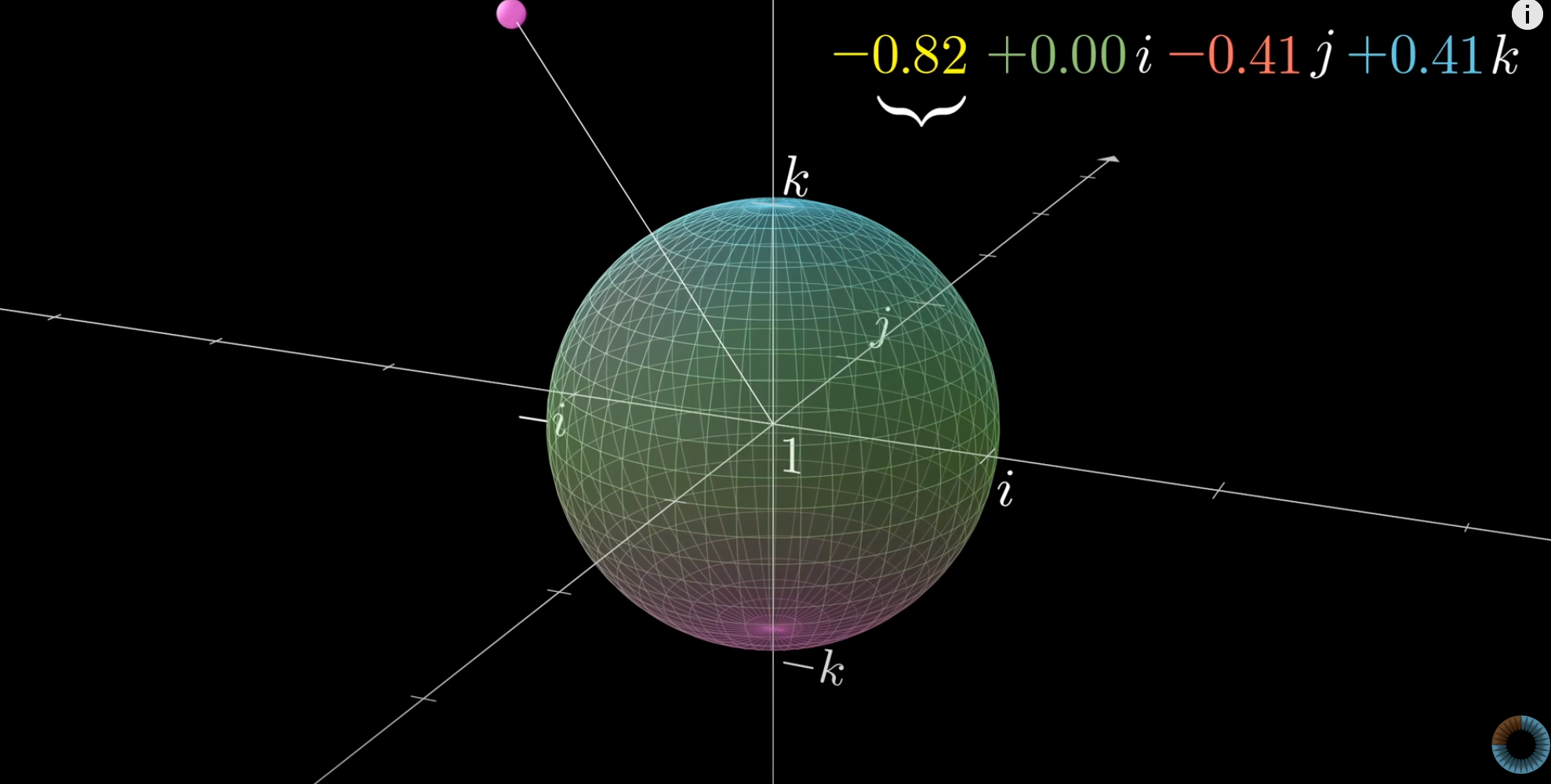
对于三维空间的任意一点，当四维世界（的单位圆）发生旋转时，是将（1,0,0,0）拉扯到该点从而发生了旋转（类比复数表示旋转）。而这一个现象在三维空间中可以理解为两个二维变换，实际上是通过一个轴向的拉伸（这个轴实际上是个圆，实部的-1到1），和一个球体的形变（临界球不再是原来四维空间的位置了）来得到的。这个推导过程可以和之前复数一致，都以ijk为轴先考虑，所以对于特定点（0，1，0，0）先乘一个i，发现它在i方向会拉伸然后回到原点（拉伸），同时j会转向k再到-j（旋转），同理将这个作为一组正交基理解，就发现它可以表达任何一个关于特定矢量为轴的旋转，把二维复数的拉伸旋转类比到四维的，发现是一模一样的变换，只是四维做的旋转操作我们无法理解，而二维的旋转清晰易懂罢了，那么就是在实部cos，虚部sin来最终实现变换效果。

这个过程可以参考https://eater.net/quaternions上大佬做的可视化结果。我们可以看到第一次左乘单位球变形了（也就是说本来映射到三维空间的东西掉到了四维空间（实部大于0去了）。同时我们也看到，确实沿着我们的基准方向旋转了对应的角度。于是再右乘一个共轭，使得ijw其从另外一个方向回到单位球的位置（说明这个点重新回到了三维空间），而基准方向的旋转再次推进了对应角度。于是这个旋转的θ就需要除以二。

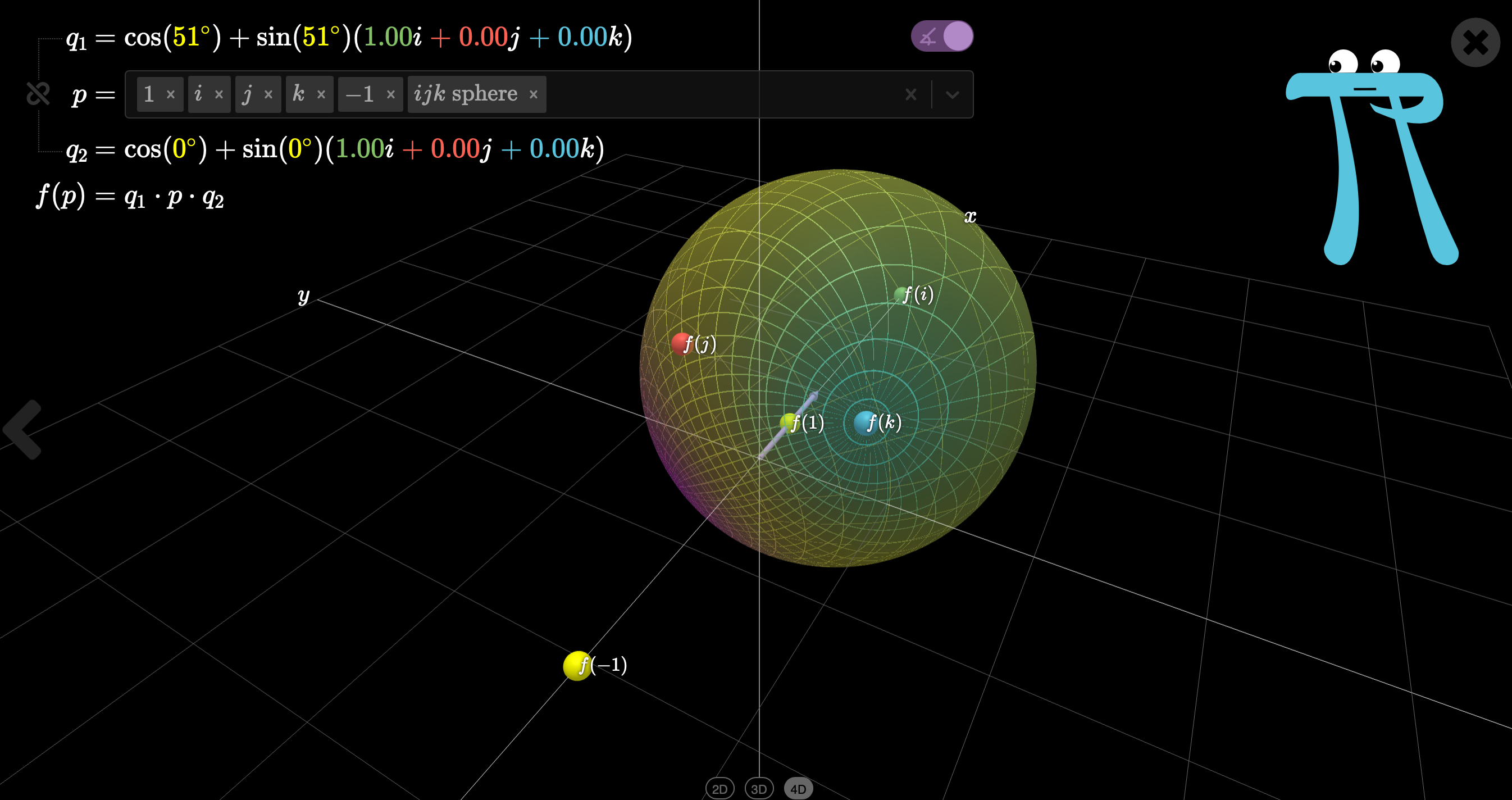
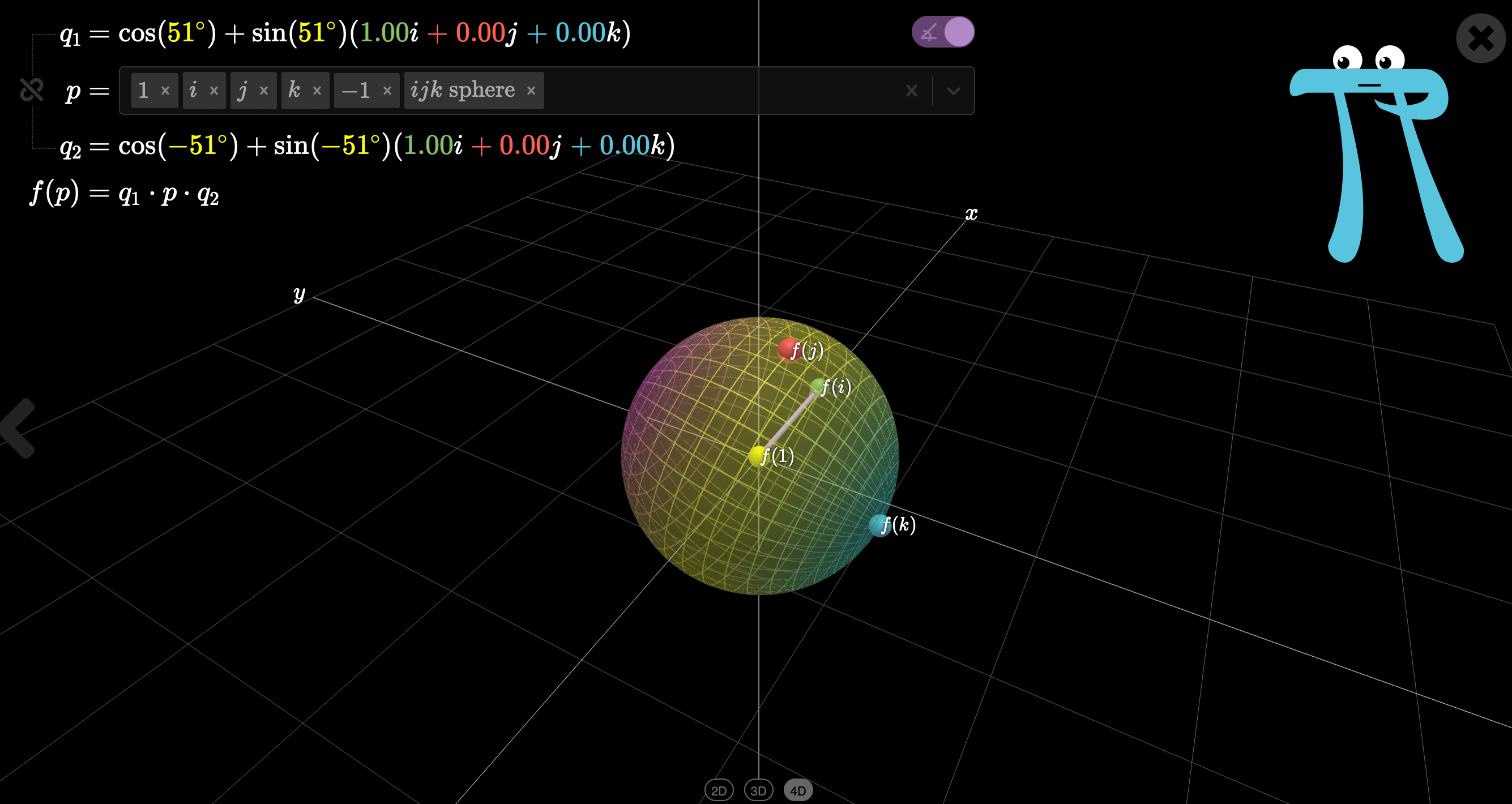
所以得到这个神奇的q四元数最终结论的值就是 q=[cosθ/2,sinθ/2 vector];

放瓦片

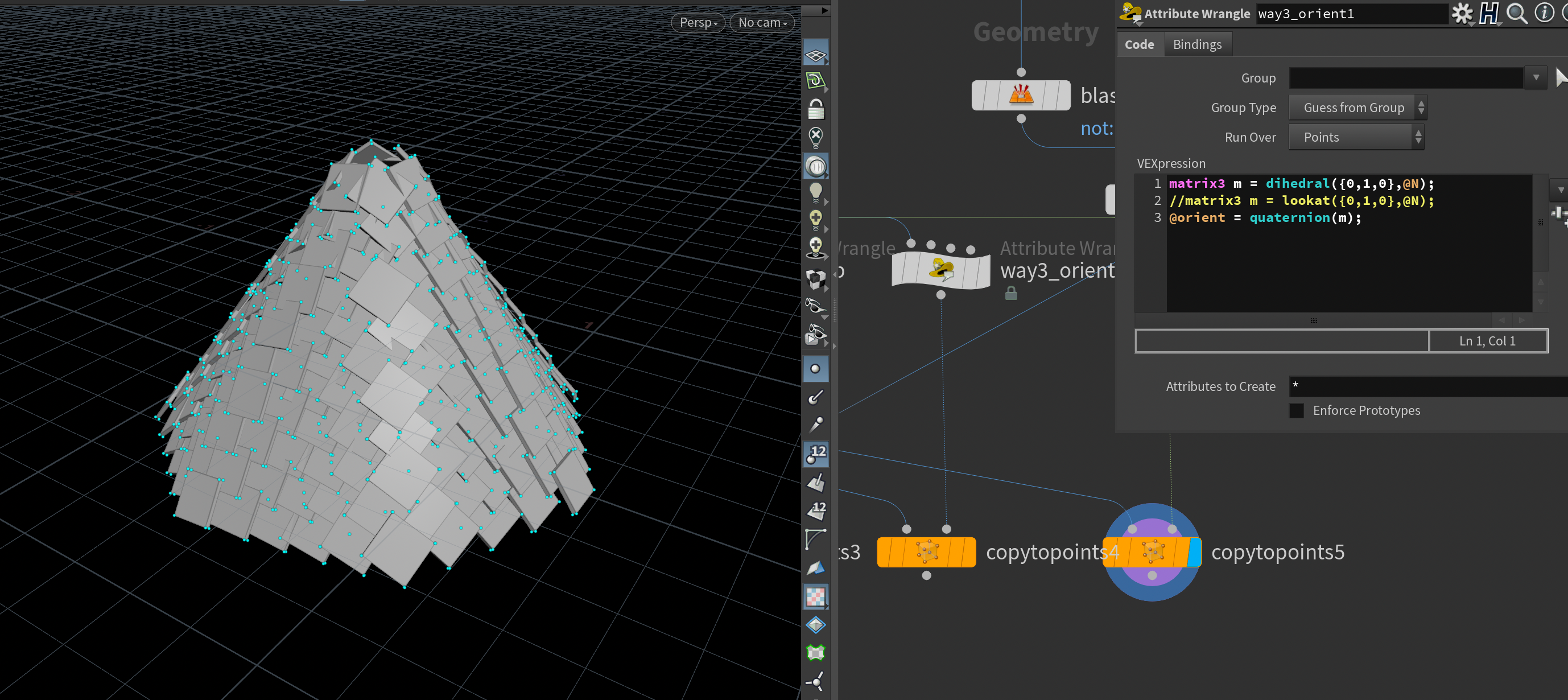
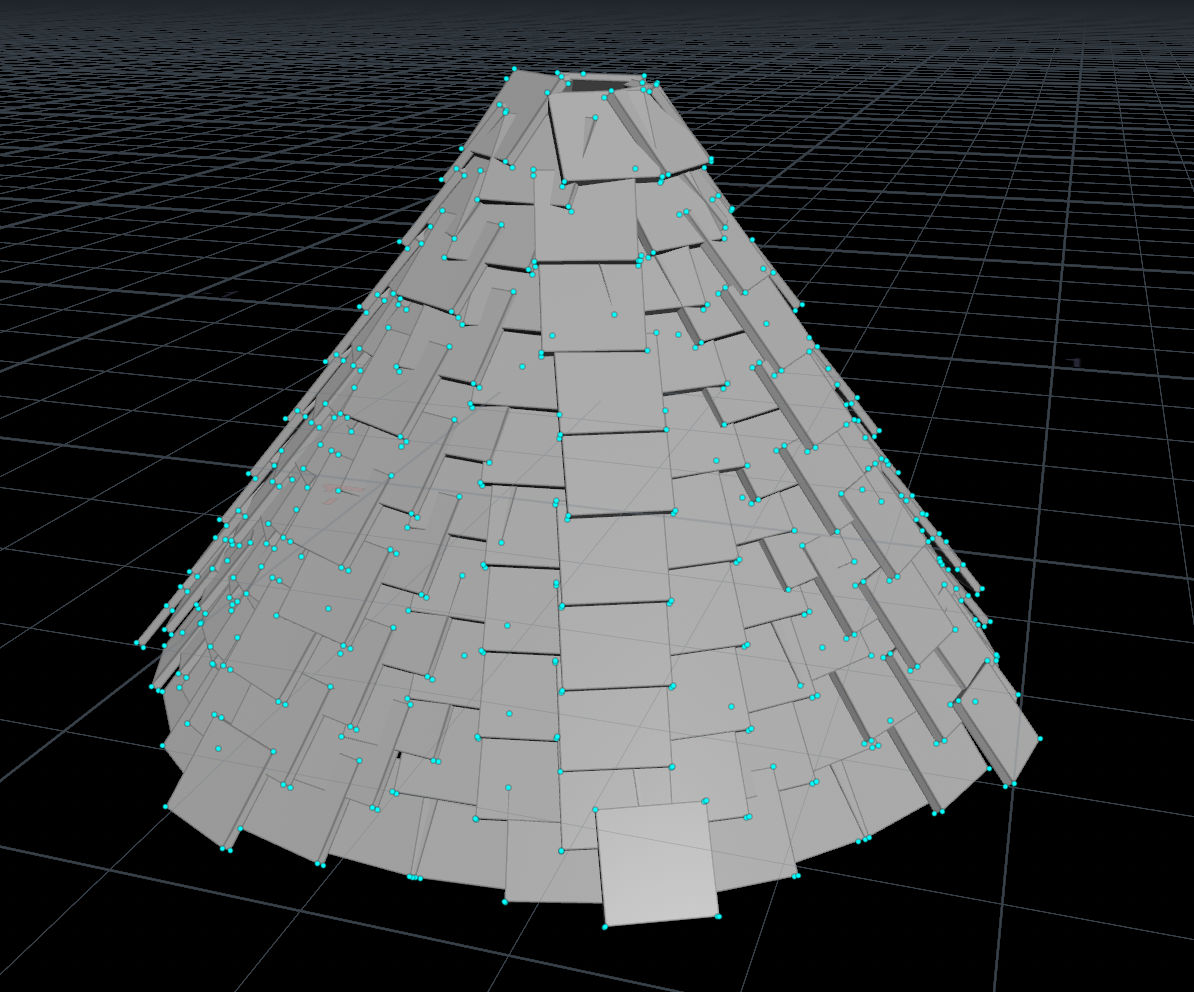
那么，让我们继续湖边小屋的塔楼瓦片搭建，一开始的做法都是用一个tube魔改顶点成cone，然后撒点做瓦片的步骤下面这个图是直接通过copytopoint，存储法线单方向后的效果。

• 第一种方法，直接通过N来控制水平方向，通过copy stamps节点（内置了一个在本地坐标系变换的功能）来实现，随机的变化值可以通过加入一些stamp解决【冬青知乎文章提到的方法就是这个】 简单补充一下copy stamp节点的功能，我可以再stamp列表中添加一个stamp variable，这里的值可以通过stamp（geometry，para name，index）实现调用，也就是你在包里甚至可以做任何的变换，stamp加参数有一系列的标准变量，可以查文档，用得最多的就是PT 代表点的序号（严格序号为TPT）然后是NCY代表复制总数。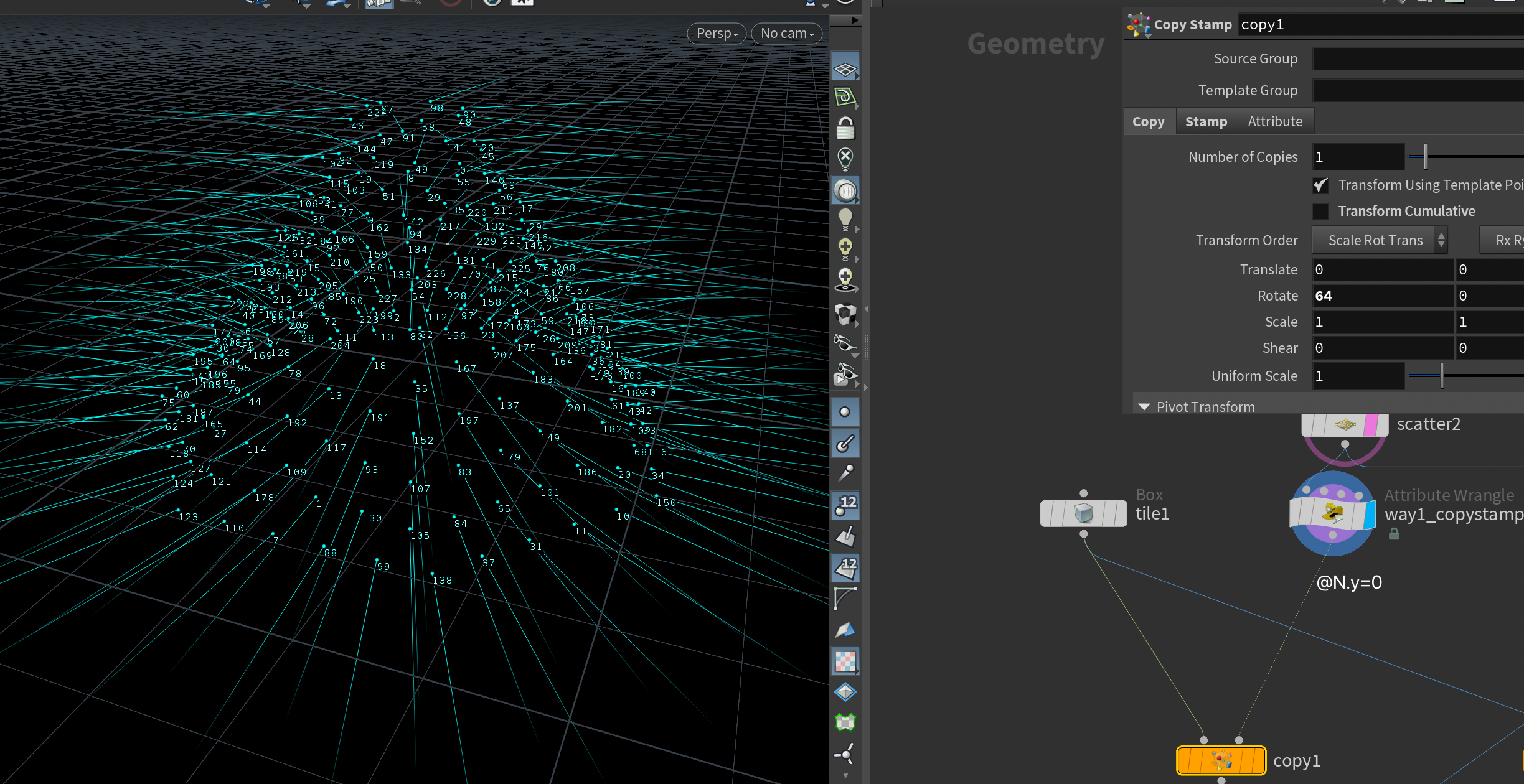

• 第二种方法，计算出一个切线出来，赋值给新变量up，然后还是用copytopoints节点，然后它自动识别旋转（甚至可以在这里搞点rand的noise，基本效果如下图）还是非常高效且令人满意的，copytopoint的变化读取的优先级为orientation然后就是N和up，前者为四元数旋转表示法则，后者就是定两个轴转过去。

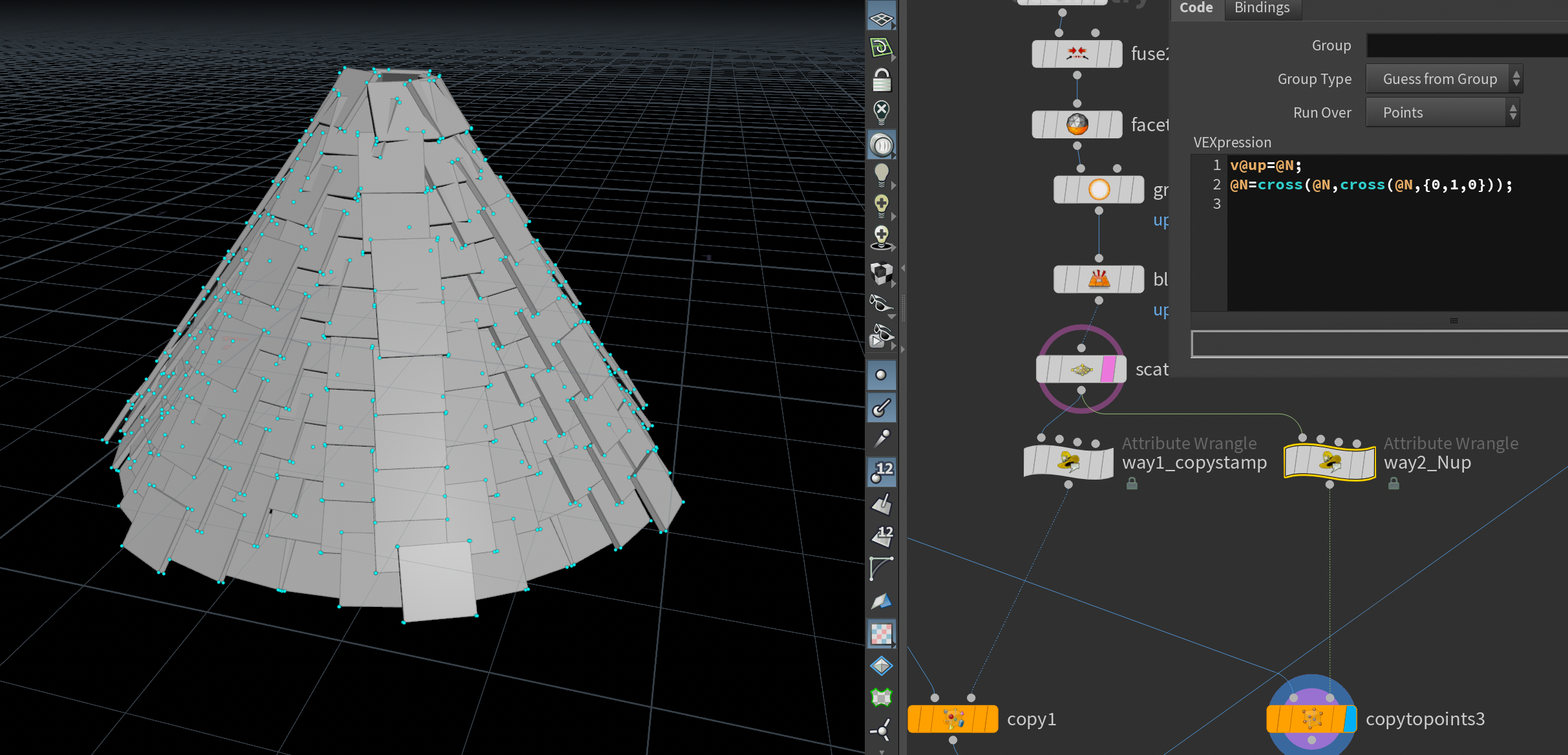
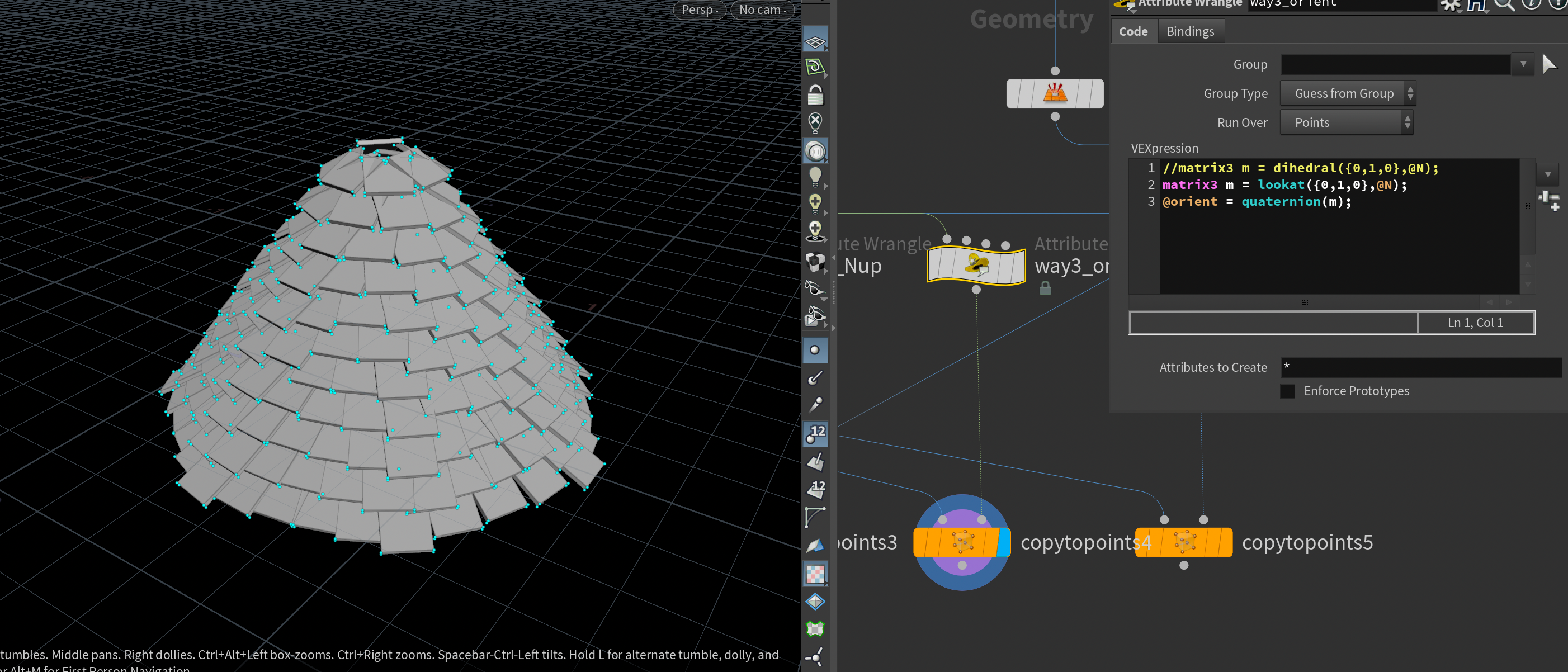
• 第三种方法，利用orient参数赋值，这里可以用两个函数来生成旋转矩阵然后用quaternion转化为四元数来进行旋转，以下是两个函数的文档说明和应用效果

  • Dihedral( ) 计算两个向量a转向b的旋转矩阵或者四元数；一般用法：将旋转角赋值一个matrix3，然后把矩阵通过四元数转化函数quaternion赋值给orient 。orientation的优先级高于up和N来定义旋转方向
  • Lookat( ) 把负z轴旋转到to-from两个向量的差值上，返回这个旋转变换矩阵，（感觉应该是和投影矩阵类似？），理论上就类似于返回一个新点和旧点的变化角度

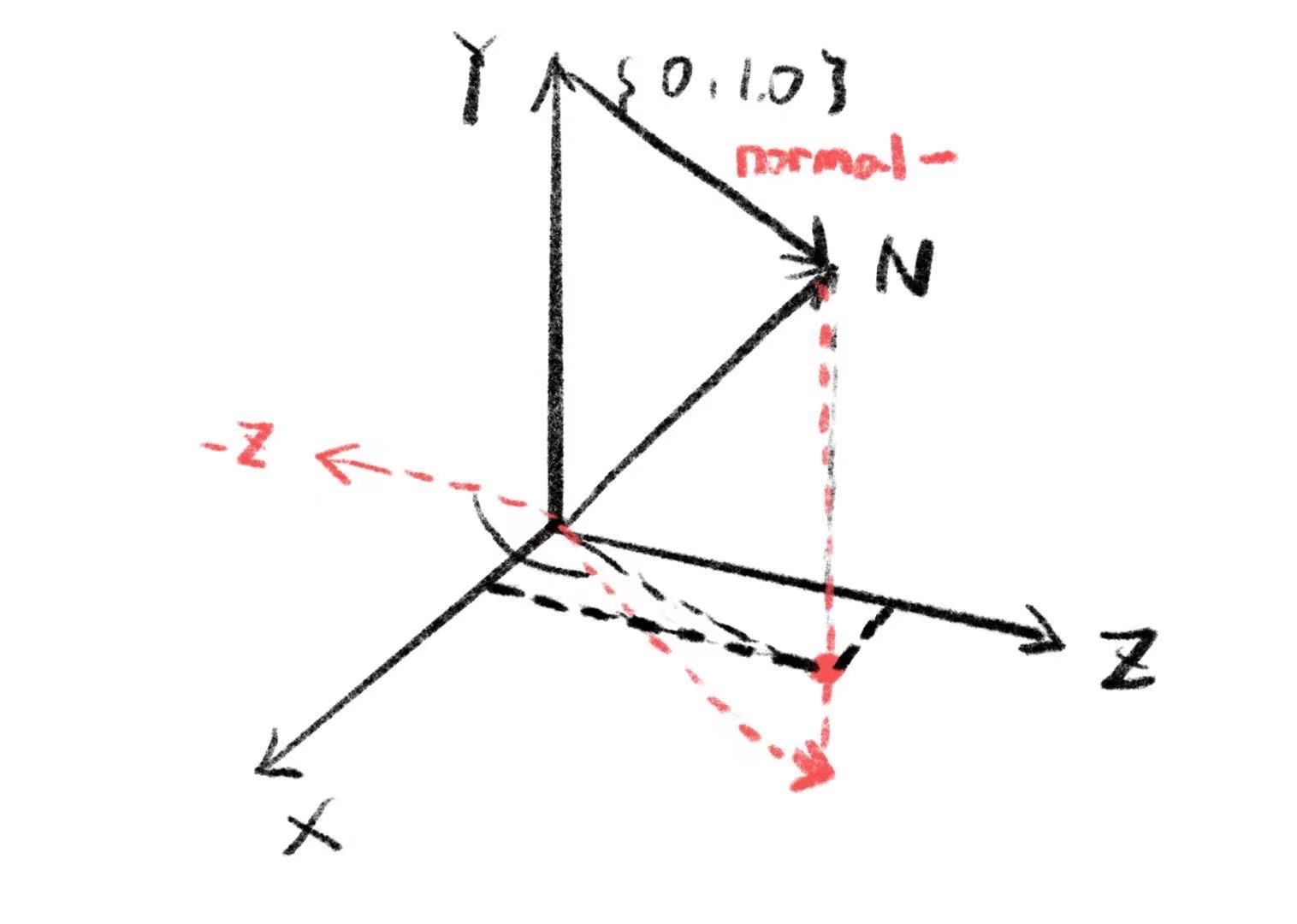
dihedral定义上非常清晰明了，而对于lookat我的理解大概应该是这样，然后-z旋转沿着y轴转的部分自然是对y轴自己无效的，然后剩下沿着NxY的那部分就刚好介于YN两个方向之间，所以图2的效果就会方向正确但是原本的N介于正确的N和Y轴之间。说明也不严格可控。

在结果上这里其实有一个问题并没解决，就是用dihedral虽然结果都是合理的（即均匀分布的旋转），但是结果的y方向转过去了，但是似乎还有一个绕自身y轴的旋转规则加进去了，这个y不是我定义的，但是看起来也不影响旋转规则，所以感觉并不是非常可控，以后有机会再来看看是否有对其进行控制的办法。

其他的旋转相关表示在VEX中的应用：

旋转矩阵的应用：直接做一个坐标轴的旋转（也就是直接用xyz轴的三个矢量set一个3矩阵）旋转的时候通过lookat或者dihedral来计算

rotate函数 对矩阵进行操作，就相当于是在自己的平移基础上乘了一个旋转矩阵（也就是按照旋转后的原点，来进行旋转，（原矩阵，弧度，轴）【主要其实用于传参数做动态】

Radian()转化弧度值

作者： Ayse